In this tutorial, you will learn what is hailstone sequence, how to write a Python program to find the hailstone sequence with and without recursion.
Let’s start with the basic algorithm to find the hailstone sequence.
Table of Contents
Example:
Input : 10
Output (Hailstone Sequence): 10 -> 5 -> 16 -> 8 -> 4 -> 2 ->1
Input : 17 Output (Hailstone Sequence): 17 -> 52 -> 26 -> 13 -> 40 -> 20 ->10 -> 5 -> 16 -> 8 -> 4 -> 2 -> 1
If you plot the graph for hailstone sequences for 10, 11, 12, 13, 14 and 15, it looks like below.
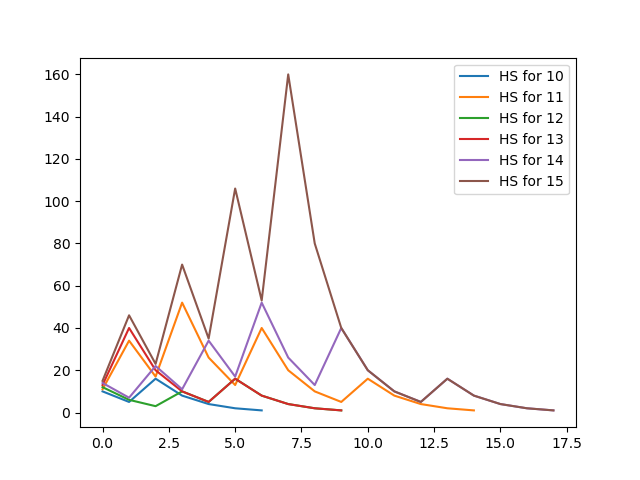
(I will share the code for piloting the graph at end of this tutorial.)
We are using Python while loop to solve this problem.
Python Program:
def hailstone_seq(start):
list_out = []
while start > 1:
list_out.append(int(start))
if start%2 == 1:
start = int(start*3+1)
else:
start = int(start/2)
list_out.append(1)
return list_out
if __name__ == "__main__":
n = input("Enter the number:")
if n.isnumeric():
n = int(n)
list_out = hailstone_seq(n)
print("Hailstone Sequence: ", list_out)
else:
print("Invalid input.")
Output:
Enter the number: 10 Hailstone Sequence: [10, 5, 16, 8, 4, 2, 1]
When you take the user input, check if the user input value is numeric or not. You can check it with the isnumeric() string method.
Other parts of the code are self-explanatory.
Hope you are familiar with the recursion programming concepts.
Python Program:
def hailstone_seq_rec(start, list_out=[]):
#base condition
if start == 1:
list_out.append(1)
return list_out
list_out.append(int(start))
if start%2 == 1:
return hailstone_seq_rec(start*3+1, list_out)
else:
return hailstone_seq_rec(start/2, list_out)
if __name__ == "__main__":
n = input("Enter the number:")
if n.isnumeric():
n = int(n)
list_out = hailstone_seq_rec(n)
print("Hailstone Sequence: ", list_out)
else:
print("Invalid input.")
Output:
Enter the number: 15 Hailstone Sequence: [15, 46, 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1]
You can find the length of the hailstone sequence simply by finding the length of the list having all the hailstone sequence numbers.
If our aim is to find only the length of the sequence, it is not efficient to store all hailstone sequence values. Instead of that, we calculate the length.
The same code we used to find the hailstone sequence can be used to calculate the length with a few lines of changes in code.
Python Program: Without using recursion (while loop)
def hailstone_seq_len(start):
len_seq = 0
while start > 1:
len_seq = len_seq+1
if start%2 == 1:
start = int(start*3+1)
else:
start = int(start/2)
return len_seq+1
if __name__ == "__main__":
n = input("Enter the number:")
if n.isnumeric():
n = int(n)
len_seq = hailstone_seq_len(n)
print("Length of Hailstone Sequence = ", len_seq)
else:
print("Invalid input.")
Output:
Enter the number:10 Length of Hailstone Sequence = 7
Python Program: Using recursion
def hailstone_seq_rec_len(start, len_seq=0):
#base condition
if start == 1:
return len_seq+1
len_seq =len_seq+1
if start%2 == 1:
return hailstone_seq_rec_len(start*3+1, len_seq)
else:
return hailstone_seq_rec_len(start/2, len_seq)
if __name__ == "__main__":
n = input("Enter the number:")
if n.isnumeric():
n = int(n)
len_seq = hailstone_seq_rec_len(n)
print("Length of the hailstone sequence = ", len_seq)
else:
print("Invalid input.")
Output:
Enter the number:15 Length of the hailstone sequence = 18
Problem statement: Write a program hailstones.py that prints all hailstone sequences with starting numbers from 1 to n and prints the number that has the longest hailstone sequence.
You have to find the seed having the maximum length of the hailstone sequence for the hailstone sequences for all the numbers in the range of given numbers.
Algorithm:
Python Program:
def hailstone_seq_len(start):
len_seq = 0
while start > 1:
len_seq = len_seq+1
if start%2 == 1:
start = int(start*3+1)
else:
start = int(start/2)
return len_seq+1
if __name__ == "__main__":
a = input("Enter the number a:")
b = input("Enter the number b:")
max_len = 0
max_seed = 0
if a.isnumeric() and b.isnumeric():
a = int(a)
b = int(b)
for i in range(a, b+1):
len_temp = hailstone_seq_len(i)
if len_temp > max_len:
max_len = len_temp
max_seed = i
print("Max length of the Hailstone Sequence is %d for seed %d." %(max_len, max_seed))
else:
print("Invalid input.")
Output:
Enter the number a: 10 Enter the number b: 15 Max length of the Hailstone Sequence is 18 for seed 14.
When I attended an interview with NVIDIA, they asked me to optimize it further.
We can use a dynamic programming approach to optimize this problem.
Let’s look at the hailstone sequence for 10 and 11.
[10, 5, 16, 8, 4, 2, 1] [11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1]
Here the total iteration to calculate hailstone sequence length will be 22.
7 (length of hailstone sequence for 10) + 15 (length of hailstone sequence for 11)= 22
How can we optimize it?
Observe the sequence for 10 and 11. The hailstone sequence for 10 is a subset of the hailstone sequence for 11.
With this optimization, we have saved the number of iterations from 22 to 15.
Python Program with Optimization:
hs_len_dict = {}
itr = 0
def hailstone_seq_len(start):
global itr
len_seq = 0
while start > 1:
itr = itr+1
if start in hs_len_dict:
return hs_len_dict[start]+len_seq
len_seq = len_seq+1
if start%2 == 1:
start = int(start*3+1)
else:
start = int(start/2)
return len_seq+1
if __name__ == "__main__":
a = input("Enter the number a:")
b = input("Enter the number b:")
max_len = 0
max_seed = 0
if a.isnumeric() and b.isnumeric():
a = int(a)
b = int(b)
for i in range(a, b+1):
len_temp = hailstone_seq_len(i)
hs_len_dict[i] = len_temp
if len_temp > max_len:
max_len = len_temp
max_seed = i
print("Max lenght of the Hailstone Sequence is %d for seed %d" %(max_len, max_seed))
else:
print("Invalid input.")
print("Number of iteration: ", itr)
Output:
The final output of the optimized code will be the same, but the process is optimized. The number of iterations required has dropped from 72 to 39.
Enter the number a: Enter the number b: Max length of the Hailstone Sequence is 18 for seed 14 Number of iteration: 39
You can also further optimize this program by calculating the square root of the number. (Hint: If the given number is a square of two, the length of the Hailstone Sequence is the square root of that number.)
We are using matplotlob library for plotting the graph. It is one of the most used Data Science Python libraries used for graph plots.
If you don’t have matplotlib library installed, you can install it using pip tool. Here is the command.
pip install matplotlib
Let’s plot the graph for hailstone sequences for 10 to 15.
Python Program:
from matplotlib import pyplot as plt
def hailstone_seq(start):
list_out = []
while start > 1:
list_out.append(int(start))
if start%2 == 1:
start = int(start*3+1)
else:
start = int(start/2)
list_out.append(1)
return list_out
if __name__ == "__main__":
a = 10
b = 15
for i in range(a, b+1):
list_out = hailstone_seq(i)
plt.plot(list_out, label='HS for %d'%i)
plt.legend()
plt.show()
Output:
Hailstone Sequence in Python is a very interesting and common problem of sequencing.
This problem has been asked in many interviews for different companies.
If you have any questions regarding the hailstone sequence problem, let’s discuss it in the comment.
I am complete Python Nut, love Linux and vim as an editor. I hold a Master of Computer Science from NIT Trichy. I dabble in C/C++, Java too. I keep sharing my coding knowledge and my own experience on <b>CSEstack.org</b> portal.
n = int(input(‘Enter the number : ‘))
while True:
if n!=1:
if n%2==0:
n = n/2
elif n%2==1:
n = n*3+1
print(n)