Dynamic Programming and Recursion | Difference, Advantages with Example

Do you want to learn dynamic programming recursion in detail?

Recursion and dynamic programming are two important programming concepts you should learn if you are preparing for competitive programming.

If you ask me what the difference is between a novice programmer and a master programmer, dynamic programming is one of the most important concepts master programmer experts understand very well.

In this tutorial, I will explain dynamic programming and how it is different from recursion with programming examples.

At the end of the tutorial, you will also learn how you can master Dynamic Programming (DP).

What is Recursion?

Recursion and dynamic programming (DP) are very dependent terms. You can not learn DP without knowing recursion.

Before getting into dynamic programming let’s learn about recursion.

Recursion is a programming technique where a programming function calls itself.

Every recursion function consists of two parts.

• code to execute in the recursive function
• termination condition or base condition

Here single function gets calls recursively until the base condition gets satisfied.

Recursion is very useful when your programs need to be divided into multiple parts and output of the one part depends on the output of the previous part.

[Example] Fibonacci Series using recursion

Let’s take an example to generate the Fibonacci series:

Fibonacci Series: 1, 1, 2, 3, 5, 8, 13, 21, 34,…

First, two numbers in the Fibonacci series are 1. After that, the next number is calculated by adding the previous two numbers in the Fibonacci series.

For more detail follow the Fibonacci series and different recursion techniques.

We can calculate this series by formulating the problem as the below algorithm. fib (n) = 1; if n < 2 fib (n) = fib(n-1) + fib(n-2)

In the first line, “n < 2” is a base condition.

The Fibonacci number is calculated using a recursive function call.

If you are calculating the nth Fibonacci number, this is what it looks like. fib(n) = fib(n-1) + fib(n-2) fib(n-1) = fib(n-2) + fib(n-3) fib(n-2) = fib(n-3) + fib(n-4) …………………………… ………………………….. ………………………….. fib(3) = fib(2) + fib(1)

The fib(n) is divided into two subproblems fib(n-1) and fib(n-2)

Further, The fib(n-1) is divided into two subproblems fib(n-2) and fib(n-3), and so on.

Calling the recursive function forms a tree.

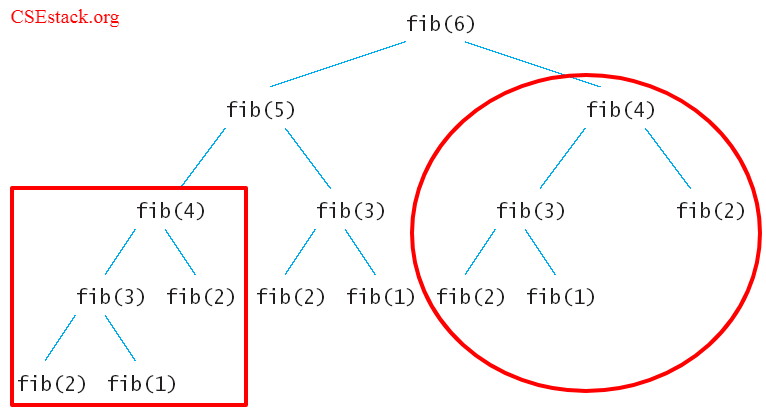
Fibonacci Series using Recursion in C:

We can write the recursive C program for the Fibonacci series.

#include<stdio.h>;
int fib (int n) {
        if (n < 2)
            return 1;
        return fib(n-1) + fib(n-2);
}
void main() {
    printf("The Fibonacci number for index 6 = %d",fib(6));
}

Output: The Fibonacci number for index 6 = 8

This is all about recursion in programming.

If you look at the above Fibonacci diagram, you can see we are calculating fib(4) twice. This puts an extra processing power to perform the same task again and again.

That’s where you need dynamic programming.

Now the question is, how dynamic programming is different from recursion?

What is Dynamic Programming Recursion?

It is one of the special techniques for solving programming questions. It is also referred to as DP in a programming contest.

DP is generally used to solve problems which involve the following steps

• Split the problem into multiple small subproblems. And keep the array of results of the small problem.
• While solving each problem, check if the same problem was solved earlier. If yes, take the result from the result array instead of solving the same subproblem again.
• Merge the subproblem result into the final result.

As we are storing the answer to every subproblem for future use, it requires extra memory to save the data. This process is called memorization.

The main intention of dynamic programming is to optimize the programming code with logic.

The problem may contain multiple similar subproblems. Every same problem is solved only at once. This reduces the overhead of extra processing.

[Example] Fibonacci Series using Dynamic Programming

Just look at the image above. In recursion, many values are repeatedly calculated like fib(4).

This gives extra processing overhead in calculating the Fibonacci value for 4.

What if we store the calculated value for fib(4) and use it next time?

Here comes the dynamic programming.

Fibonacci Series using a Dynamic Programming approach with memoization.

include<stdio.h>;
int fib (int n) {
        arrFib[100] = {0};
        arrFib[0] = 1;
        arrFib[1] = 1;
        for (int i = 2; i<n; i++)
           arrFib[i] = arrFib[i-1] + arrFib[i-2];
       return arrFib[n-1]
    }
void main() {
    printf("The Fibonacci number for index 6 = %d",fib(6));
}

Output: The Fibonacci number for index 6 = 8

Instead of calling the function recursively, we are calculating the value of the Fibonacci series and storing it in a database array (memoization technique).

Here in Dynamic Programming, we trade memory space for processing time.

Difference between recursion and dynamic programming

What is the difference between these two programming terms?

If you look at the final output of the Fibonacci program,  both recursion and dynamic programming do the same things.

But logically both are different during the actual execution of the program.

Advantages of Dynamic Programming over recursion

• As it is a recursive programming technique, it reduces the line code.
• One of the major advantages of using dynamic programming is it speeds up the processing as we use previously calculated references.

Disadvantages of Dynamic Programming over recursion

It comes with certain disadvantages.

• It takes a lot of memory to store the calculated result of every subproblem without ensuring if the stored value will be utilized or not.
• Many times, the output value gets stored and never gets utilized in the next subproblems while executing. It leads to unnecessary memory utilization.
• In DP, functions are called recursively. Stack memory keeps increasing.

When to use which?

First, understand the idea behind the DP.

• Divide the problem into multiple subproblems and save the result of each subproblem.
• If the same subproblem occurs, rather than calculating it again, we can use the old reference from the previously calculated subproblem.
• Once we have calculated the result for all the subproblems, conquer the result for the final output.

Now, decide what should you use in your program.

• If you have limited memory to execute the code and are not bothered about processing speed, you can use recursion. Ex. if you are developing a mobile application, memory is very limited to execute your application.
• If you want to execute your program faster and don’t have any memory constraints, use dynamic programming.

Recursion and dynamic programming are very important concepts if you want to master any programming language.

These are generic concepts and you can see them in almost all generic programming languages. There might be a syntactic difference in defining and calling a recursive function in different programming languages.

How to Learn and Master DP?

To solve the dynamic programming problem you should know the recursion. Get a good grip on solving recursive problems. The Fibonacci series is one of the basic examples of recursive problems.

The theory of dividing a problem into subproblems is essential to understand.  Learn to store the intermediate results in the array.

You can heighten your understanding by knowing how it has been used in many of the DP problems and practices.

Among all the points discussed here to become the expert in the DP problem, practicing is on top.

Solve as many problems as you can. It will give you a significant understanding and logic building for dynamic problems.

DP comes in very handy in competitive programming. Practice solving programming questions using recursion. And then optimize your solution using a dynamic programming technique.

Dynamic Programming Recursion Examples for Practice:

These are some of the very basic DP problems.

• Fibonacci Series
• Traveling Salesman Problem
• All Pair Shortest Path (Floyd-Warshall Algorithm)
• 0/1 Knapsack Problem using Dynamic Programming
• Matrix Chain Product/Multiplication using Dynamic Programming
• Longest Common Subsequence (LCS) using Dynamic Programming

There is a huge list of dynamic problems. Solve regularly.

As per your schedule, you can plan to solve one DP problem per day. If you have more time you can go to solving multiple DP problems per day.

Most importantly, don’t hurry to solve the DP problem and skip your understanding of it.

In the end, it does not matter how many problems you have solved. It is just a matter of how you understand it.

This is all about the differences and advantages of dynamic programming recursion. If you have any doubt on this topic let’s discuss it in the comment.

Happy Programming!

Aniruddha Chaudhari

I am a Python enthusiast who loves Linux and Vim. I hold a Master of Computer Science degree from NIT Trichy and have 10 years of experience in the IT industry, focusing on the Software Development Lifecycle from Requirements Gathering, Design, Development to Deployment. I have worked at IBM, Ericsson, and NetApp, and I share my knowledge on CSEstack.org.