QuickSort Complete Tutorial | Example | Algorithm | Programming | Complexity

In this tutorial, I will explain the QuickSort Algorithm in detail with the help of an example, algorithm and programming. To find out the efficiency of this algorithm as compared to other sorting algorithms, at the end of this article, you will also learn to calculate complexity.

Without any ado, let’s start.

Introduction to QuickSort:

What is a Quick Sort?

Quick Sort is based on the concept of divide-and-conquer, just the same as merge sort. The basic idea of quicksort is to pick an element called the pivot element and partition the array. The quicksort algorithm is also known as a partition-exchange algorithm.

The partition in quicksort divides the given array into 3 parts:

• Elements less than the pivot element
• Pivot element
• Elements greater than the pivot element

You might be wondering what a pivot element is. A pivot element is that element which is used to partition the array, i.e. it can be the last element, the first element or any random element.

For example, Consider an array of elements.

X= {72, 23, 12, 65, 87, 52, 33, 46}

Here we pick up 46 as the pivot element (i.e. the last element in the array).

Now, after the first pass the, the array will look like-

X= {23, 12, 33, 46, 87, 52, 72, 65}

Here, the pivot is set at its position while all the elements that are smaller than the pivot are placed to its left and the elements greater than the pivot are placed to its right.

So, at the instant {23, 12, 33} and {87, 52, 72, 65} are two sub-arrays and the recursive logic of partitioning elements (dividing the array) with the help of pivot element and keep doing this until and unless the array is sorted completely.

How does Quick Sort work?

1. Pick an element, called a pivot or refer it as the partitioning element, from the array. For instance, let us consider the last element as a pivot.
2. Partition: rearrange the array such that all elements with values less than the pivot come before the pivot (i.e., on the left of the pivot), while all elements with values greater than the pivot come after it (i.e., on the right of pivot). The pivot element will be in its final position after it.
3. Recursively apply the above steps to the sub-array of elements on the left side of the pivot and on the right side of the pivot to get a sorted array.

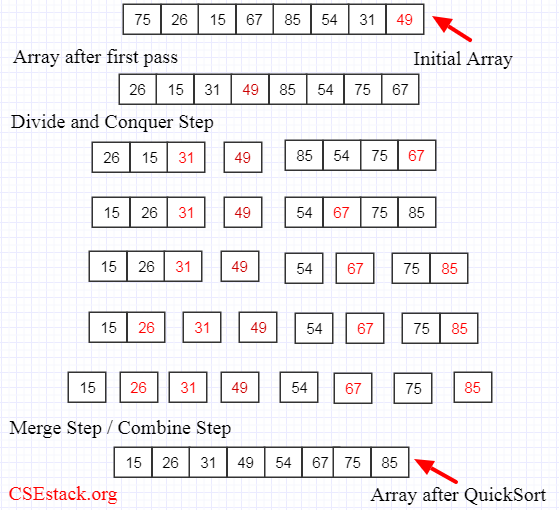
Now, using pictorial representation, let’s try to sort an array which has initial values as X= {75, 26, 15, 67, 54, 31, 49}.

Here, in the above representation, we select the element at the last index of the array as a pivot, which is 49 and then call partition() to thereby re-arrange the elements of the array in a way that elements less than 49 are before it in and elements greater than 49 are after it.

Then, after the first pass, we consider the subarrays at left and right and select a partition element for them. Here, in the above representation, we select 31 as a pivot from the left array and 67 as a pivot from the right array. And once again call the partition() to split the array.

Thus, we recursively keep partitioning the array with help of pivot unless we obtain a sorted array.

How to implement the QuickSort algorithm?

The below function can be used as a recursive approach to sort elements using Quick Sort.

QuickSort(A,start,end){
	if(start >= end){
           //calling partition function
           pIndex <- Partition(A,start,end);	
           QuickSort(A, start, pIndex-1);
           QuickSort(A,pIndex+1,end);
         }
}

The below function describes how partitioning is performed using the pivot element–

Partition(A, start, end){
 pivot <- A[end];
 pIndex <- start;
 for i<- start to end
 {
	if(A[i] <= pivot){
	    swap(A[i], A[pIndex]); // a function to swap the elements
	    pIndex <- pIndex + 1;
	}
  }
  swap(A[pIndex],A[end]);
  return pIndex;
}

QuickSort Programming:

If you understand the working of QuickSort algorithm, it is not much difficult to convert the QuickSort algorithm into the code for different programming languages.

I have added comments in the code wherever needed. Most of the code is self-explanatory.

C/C++ Programming:

/* C program for QuickSort implementation*/
#include

//swapElement is utility function to swap two elements
void swapElements(int* a, int* b)
{
	int t = *a;
	*a = *b;
	*b = t;
}

//This fucntuin puts all the smaller elements at left 
//and bigger elements at right of the pivot element 
//in the array
int partition (int nArray[], int nStart, int nEnd)
{
        //Choosing last element as pivot
	int pivot = nArray[nEnd];

        //Index of smaller element 
	int i = (nStart - 1); 

	for (int j = nStart; j <= nEnd- 1; j++)
	{
		// If current element is smaller than or
		// equal to pivot
		if (nArray[j] <= pivot)
		{
			i++; // increment index of smaller element
			swapElements(&nArray[i], &nArray[j]);
		}
	}
	swapElements(&nArray[i + 1], &nArray[nEnd]);
	return (i + 1);
}

/* Function to QuickSort the array
nArray[] - Input array to sort,
nStart - Starting index of nArray,
nEnd - Ending index of nArray */
void QSort(int nArray[], int nStart, int nEnd)
{
	if (nStart < nEnd)
	{
		//Here, pivot is partitioning index, 
		//nArray[pivot] is now at right place
		int pivot = partition(nArray, nStart, nEnd);

		//Recursive call to QuickSort the elements 
		//in the array after partition
		QSort(nArray, nStart, pivot - 1);
		QSort(nArray, pivot + 1, nEnd);
	}
}

//Simple function to print 
//the elements of an array
void printArray(int nArray[], int size)
{
	int i;
	for (i=0; i < size; i++)
		printf("%d ", nArray[i]);
}

// Main function for QuickSort
int main()
{
	int arrSample[] = {75,26,15,67,85,54,31,49};
	int nSize = sizeof(arrSample)/sizeof(arrSample[0]);
	
	printf("\nInitial Array to Sort: ");
	printArray(arrSample, nSize);
	
	QSort(arrSample, 0, nSize-1);
	
	printf("\nArray after QuickSort: ");
	printArray(arrSample, nSize);

	return 0;
}

Output of C/C++ QuickSort Program

Initial Array to Sort: 75 26 15 67 85 54 31 49 
Array after QuickSort: 15 26 31 49 54 67 75 85

Python Programming:

# Python program for Quicksort

#This fucntuin puts all the smaller elements at left 
#and bigger elements at right of the pivot element 
#in the array
def partition(nArray,nStart,nEnd):
    # index of smaller element
	i = ( nStart-1 )		 
	# pivot
	pivot = nArray[nEnd]	 

	for j in range(nStart , nEnd):

		# If current element is smaller than or
		# equal to pivot
		if nArray[j] <= pivot:
		
			# increment index of smaller element
			i = i+1
			nArray[i],nArray[j] = nArray[j],nArray[i]

	nArray[i+1],nArray[nEnd] = nArray[nEnd],nArray[i+1]
	return ( i+1 )

#Function to QuickSort the array
#nArray[] - Input array to sort,
#nStart - Starting index of nArray,
#nEnd - Ending index of nArray */

def QSort(nArray,nStart,nEnd):
	if nStart < nEnd:

		# pivot is partitioning index, 
		#nArray[pivot] is now at right place
		pivot = partition(nArray,nStart,nEnd)

		#Recursive call to QuickSort the elements 
		#in the array after partition
		QSort(nArray, nStart, pivot-1)
		QSort(nArray, pivot+1, nEnd)

#QuickSort program runs from here
nArray = [75, 26, 15, 67, 85, 54, 31, 49]
nSize = len(nArray)
print("Initial Array to Sort:");
for i in range(nSize):
	print ("%d" %nArray[i]),
	
QSort(nArray,0,nSize-1)

print("\nArray after QuickSort:")
for i in range(nSize):
	print ("%d" %nArray[i]),

Note: The nArray mentioned in the above Python program is Python list. So, don’t get confused with the name.

Output of Python QuickSort Program

Initial Array to Sort:
75 26 15 67 85 54 31 49 
Array after QuickSort:
15 26 31 49 54 67 75 85

Java Programming:

Now, have a look at how quicksort is implemented using a Java program.

public class QSort {
    void swap(int a1,int a2){
        int temp = a1;
        a1=a2;
        a2=temp;
     }

     void QuickSort(int A[],int start,int end){

         if(start <= end){
             //calling partition function
             int pIndex =Partition(A,start,end);

              QuickSort(A, start, pIndex-1);
              QuickSort(A,pIndex+1,end);
         }
    }

    int Partition(int A[],int start,int end){

        int pivot= A[end];
        // set the partition index as start initially
        int pIndex = start;        

         for (int i=start;i<end;i++)
         {

              // swap if element is smaller than pivot
              if(A[i] <= pivot){

                  int temp=A[i];
                  A[i]= A[pIndex];
                  A[pIndex] = temp;
                  pIndex =pIndex + 1;
                }
             }

    //Perform swapping operation with 
    //the element at the partition index
     int t = A[pIndex];
     A[pIndex]= A[end];
     A[end] = t;
    return pIndex;
    }

    public static void main(String []args){
    int arr[] = {75,26,15,67,85,54,31,49};
    QSort obj = new QSort();
    obj.QuickSort(arr,0,7);

    for(int i:arr){
    System.out.print(i);
     System.out.print(" ");
     }             
    }
}

Output of Java QuickSort Program:

15 26 31 49 54 67 75 85

Time Complexity of QuickSort:

The equation to calculate the time taken by the Quicksort to sort all the elements in the array can be formulated based on the size of the array.

In every partition, the array is divided into two subarrays.

Best Case Time Complexity:

Let’s take the best case:

Best case occurs when the middle element gets selected for every partition.  The array is get divided into the two equal size subarray.

So the time complexity can be formulated as,

T(n) = T(n/2) + T(n/2) + Cn

Where T(n) is time taken by QuickSort to sort the array of size n elements.
C is some other constant.

So the equation becomes

T(n) = 2T(n/2) + Cn

Above recursive formula can be resolved in time O(nlog(n).

Worst Case Time Complexity:

Worst case complexity occurs when the pivot elements get selected at the end of the array every time while partitioning.

So the array will get partition into two subarray having elements (n-1) and 1.

So the time complexity equation in the worst case is

T(n) = T(n-1) + T(1) + C

After solving above recursive function, it is equivalent to

T(n) = O(n^2)

Note: Unlike to all the major sorting algorithms, QuickSort takes more time if the input array is already sorted.

Average Case Time Complexity:

In the average case, you have to consider all the possible position for choosing pivot element. It is not easy to calculate.

If we calculate the recursive solution for all the possible pivot, it is equivalent to O(nLog(n)),So the complexity.

Other Sorting Algorithm you should try to improve your coding skill.

• Write a program to check if the array is sorted. (C/C++)
• Selection Sort (Python, C/C++)
• Bubble Sort (C/C++)

I would recommend trying implementing the quicksort algorithm yourself. You can always refer to the code mentioned in this tutorial. Let us know if you have any queries.

Happy Learning!