Selection Sort in C with Explanation | Algorithm, Program and Time Complexity

There are many sorting algorithms to sort the elements in the array. Some of the simple and widely used algorithms are as follows.

• Bubble Sort
• Quick Sort
• Insertion Sort
• Selection Sort

In this C programming tutorial, we see the program for selection sort in C with explanation in detail.

What is Selection Sort?

Selection sort is an algorithm where we keep finding the smallest element and then we order them in sequence.

Stepwise Explanation for Selection Sort Algorithm:

1. Keep a pointer to the first element of the array (says i).
2. Select the smallest element from the array.
3. Replace the smallest element with the array element placed at position ‘i’.
4. Increment ‘i’ to point it to next element in the array.
5. Repeat step 2, 3 and 4 until ‘i’ reaches to the last element in an array.

Selection sort is the in-place sorting algorithm, Why?

Selection sort is the in-place sorting algorithm. It takes a constant amount of space and does not require any auxiliary data structure for sorting.  However, it uses very small amount of memory to replace the elements.

Selection Sort Program in C:

[cpp]
#include<stdio.h>

int main()
{
int nArr[]={5,35,5,31,56};
int nSize = sizeof(nArr)/sizeof(int);//5
int nMin=0;
int t=0, i=0, j=0;

printf("\nGiven Array:");
for(i=0;i<nSize;i++)
{
printf(" %d", nArr[i]);
}

//sort array using selection sort
for(i=0; i<nSize-1 ;i++)
{
nMin=i;
for(j=i+1; j<nSize;j++)
{
if(nArr[j]<nArr[nMin])
nMin = j;
}

t=nArr[i];
nArr[i]=nArr[nMin];
nArr[nMin]=t;
}

printf("\n\nSorted Array:");

for(i=0;i<nSize;i++)
{
printf(" %d", nArr[i]);
}
printf("\n");
return 0;
}
[/cpp]

Note: We have assigned elements to the array in the program itself. You can take the array elements as user input as well.

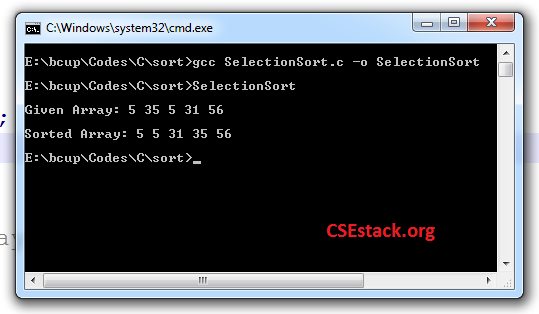
The output of a Program:

Given Array: 5 35 5 31 56
Sorted array: 5 5 31 35 56

This program and algorithm sort the array in ascending order.

If you want to sort the array in descending order, (step 2 in the algorithm) find the largest element rather than the smallest element.

The time complexity of the Selection Sort algorithm:

If you look at steps 2, 3, 4 and 5 iterates ‘n’ number of times. (Where n is a number of elements in the array (array size).) . So iterations take O(n) time.

Within each iteration,  you have to find out smallest element in the array. It takes the complexity of O(n).

So the total complexity of the Selection sort algorithm is O(n)* O(n)  i.e. O(n^2).

Worst Case Complexity: O(n^2)

Best Case Complexity: O(n^2)

Average Case Complexity: O(n^2)

Here, all three complexity will be the same.

In the best case, we consider as the array is already sorted. But to find out the smallest element, we need to iterate and check for all the elements in the array. So the best complexity is the same a worst case complexity.

You can also check if the array is already sorted before applying selection sort. In the best case, it saves your program execution time.

Comparing with other sorting algorithms:

Selection sort is easiest to implement and to code than other sorting algorithms. But, it is not much efficient in terms of time complexity.

Advantages of this selection sort:

• Easily understood.
• Easiest to implement and to code.
• No extra space is required (in-place sorting)

The drawback of selection sort:

• It has very high time complexity. (O(n^2) in all three cases.)

Note: For most efficient algorithm as per time complexity, you can use heap or merge sort. They have O(n log(n)) time complexity.

This is all about Selection Sort in C with Explanation. If you have any doubt feel free to write in a comment.

Happy Programming!

Aniruddha Chaudhari

I am a Python enthusiast who loves Linux and Vim. I hold a Master of Computer Science degree from NIT Trichy and have 10 years of experience in the IT industry, focusing on the Software Development Lifecycle from Requirements Gathering, Design, Development to Deployment. I have worked at IBM, Ericsson, and NetApp, and I share my knowledge on CSEstack.org.