The problem of tower of Hanoi was brought in 1883 by M.Claus (Lucas). It consists of disks and three pegs.
It is one of the vary popular example in data structure.
Tower of Hanoi Puzzle:
All the disks have different diameters and holes in the middle.
They are placed over one another in such an order that the disk with the largest diameter is placed on the bottom and the disk with smaller is placed above and so on.
The disk with the smallest diameter is placed at the top.
Table of Contents
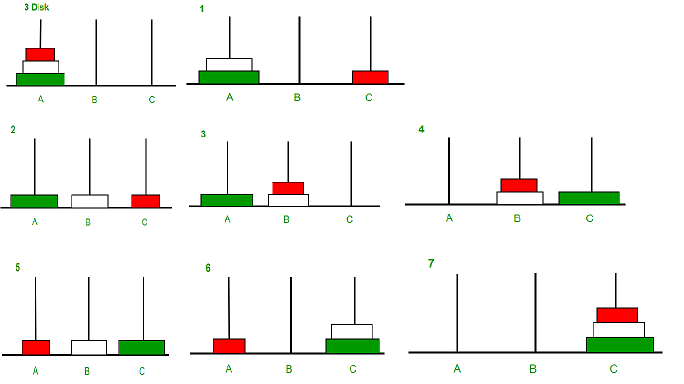
Let us discuss the problem by considering three disks.
Initially, all the disks are placed over one another on the peg A. Our objective is to shift all the disks from peg A to peg C using intermediate peg B.
There are some rules to solve this problem.
Here is how you can solve the Tower of Hanoi problem for three disk.
In case of three disks you can find the solution manually but for a larger number of disks like four or more than four then the situation becomes quite complex.
The problem has a recursive nature which leads to a straight forward recursive solution.
Assume there are N disks, if N=1, then you simply shift the disk from peg A to peg C.
When N>1, then you can divide the original problem into three subproblems and solve them sequentially as follows.
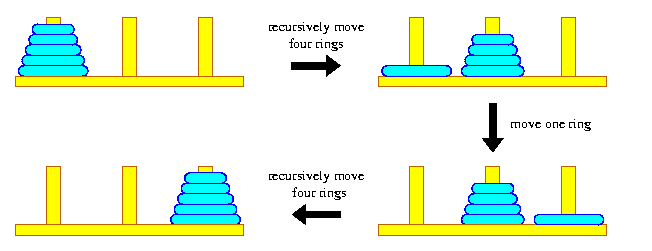
We can solve this problem by using recursion.
Algorithm to solve Tower of Hanoi puzzle using recursion:
MOVE(N, SRC, INT, DEST)- This algorithm shifts (N>0) number of disks from source peg (SRC) to destination peg (DEST) using the intermediate peg (INT).
1. If (N=1) then //shifting a single disk
Write "shift single disk from "SRC "to" DEST
Else //shifting N-1 disk recursively
a) MOVE (N-1,SRC,DEST,INT)
b) DEST<-SRC //shift disk from SRC peg to DEST peg
c) MOVE(N-1,INT,SRC,DEST)
//end of if structure
2. Return.
If you understand the algorithm it’s pretty easy to implement the Tower of Hanoi problem with recursion.
Prerequisite:
Program to solve Tower of Hanoi:
def hanoi(disks, source, auxiliary, target):
if disks == 1:
print('Move disk 1 from peg {} to peg {}.'.format(source, target))
return
hanoi(disks - 1, source, target, auxiliary)
print('Move disk {} from peg {} to peg {}.'.format(disks, source, target))
hanoi(disks - 1, auxiliary, source, target)
disks = int(input('Enter number of disks: '))
hanoi(disks, 'A', 'B', 'C')
Output
Case 1: when number of disk is 4
Enter number of disks: 4 Move disk 1 from peg A to peg B. Move disk 2 from peg A to peg C. Move disk 1 from peg B to peg C. Move disk 3 from peg A to peg B. Move disk 1 from peg C to peg A. Move disk 2 from peg C to peg B. Move disk 1 from peg A to peg B. Move disk 4 from peg A to peg C. Move disk 1 from peg B to peg C. Move disk 2 from peg B to peg A. Move disk 1 from peg C to peg A. Move disk 3 from peg B to peg C. Move disk 1 from peg A to peg B. Move disk 2 from peg A to peg C. Move disk 1 from peg B to peg C.
Case 2: when number of disk is 2
Enter number of disks: 2 Move disk 1 from peg A to peg B. Move disk 2 from peg A to peg C. Move disk 1 from peg B to peg C.
Case 3: when number of disk is 1
Enter number of disks: 1 Move disk 1 from peg A to peg C.
Try giving a different number of dicks as user input and check the output. This simple recursive solution works for any number of disks.
Did you observe the number of minimum disks move required to solve the Tower of Hanoi problem?
Lets find it programmatic way.
count = 0
def hanoi(disks, source, auxiliary, target):
global count
if disks == 1:
count = count + 1
return
hanoi(disks - 1, source, target, auxiliary)
count = count + 1
hanoi(disks - 1, auxiliary, source, target)
disks = int(input('Enter number of disks: '))
hanoi(disks, 'A', 'B', 'C')
print("Minimum number of disks move: ", count)
Output:
Case 1: when number of disks are 3
Enter number of disks: 3 Minimum number of disks move: 7
Case 2: when number of disks are 5
Enter number of disks: 5 Minimum number of disks move: 31
Look at the minimum number of disks (as an output) for a given number of disks.
If n is the number of the disks, then it requires (2^n)-1 number of disk moves to solve the problem.
I hope you understand the Tower of Hanoi problem and how to solve it using recursion. If you have any questions, you can ask me in the comment. Keep learning!
I'm pursuing a bachelor's in engineering in Information technology from Chandigarh University. I have deep interest in Data structure , Optimization technique , Python and Mathematics. I find heaven in my books