Level Order Traversal in Binary Tree | Explained with Code and Example

Traversal is an algorithm for visiting each node in a different fashion. Earlier we have seen see pre-order, in-order and post-order BT traversal.

Now we are interested in level order traversal.

What is level order traversal in Binary Tree?

In level order traversal, we visit (print) nodes of the binary tree at level zero, then at level one, two and so on…

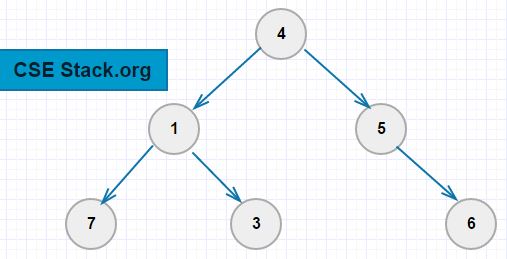
For the above binary tree, the level order traversal is 4, 1, 5, 7, 3, 6.

• The node at level one is 4.
• The node at level two is 1 and 5.
• The node at level three is 7, 3, 6.

Note: The number of levels in the binary tree is one more than the height of the tree (or root node). In the above example, the height of the BT is two and the total number of levels is three (2+1).

Algorithm

1. Find the height of the binary tree
2. Repeat for each level (1 to height+1)
- Print the value of nodes at that level. 
  (Use recursion here to print the values.)

To implement level order traversal, it is required to find the height of a Binary Tree.

Python Program

Here is a simple Python program for level order traversal using recursion.

[python]
class node:
def __init__(self, val, left=None, right=None):
self.left=left
self.val=val
self.right=right

def height(root):
if root:
return 1+max(height(root.left), height(root.right))
else:
return -1

def printAtLevel(root, level):
if root:
if level==1:
print(root.val)
else:
printAtLevel(root.left, level-1)
printAtLevel(root.right, level-1)

def levelOrderTraversal(root):
for i in range(1,height(root)+2):
printAtLevel(root, i)

root=node(4)
root.left=node(1)
root.right=node(5)
root.left.left=node(7)
root.left.right=node(3)
root.right.right=node(6)
levelOrderTraversal(root)
[/python]

Output:

4
1
5
7
3
6
8

If Python is not your primary language, try to solve this problem in C/C++, Java or any programming language you are comfortable with. You can use the same algorithm and logic.

Complexity

The worst-case complexity of the algorithm is with a skewed binary tree where each node will be having either one or two nodes.

In the skewed tree, to print the element at level one (function printAtLevel()) take the time of O(1), to print the element at level two takes the time of O(2)… to print the element at level n takes the time of O(n)…

(Where, n is the number of nodes in the binary tree.)

To print all the elements at each level is O(1)+O(2)+O(3)+…+O(n)=O(n^2).

So, in the worst case, the time complexity of level order traversal in binary tree is O(n^2).

Aniruddha Chaudhari

I am a Python enthusiast who loves Linux and Vim. I hold a Master of Computer Science degree from NIT Trichy and have 10 years of experience in the IT industry, focusing on the Software Development Lifecycle from Requirements Gathering, Design, Development to Deployment. I have worked at IBM, Ericsson, and NetApp, and I share my knowledge on CSEstack.org.