Program to Find the Height of the Binary Tree using Recursion

What is the Height of Binary Tree (BT)?

The height of the Binary Tree is the number of edges from the root node to the deepest leaf node.

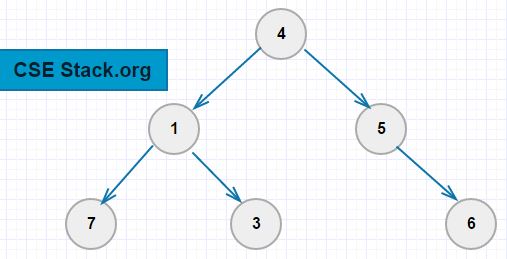
The height of the tree is the same as the height of the root node.

In the above binary tree,

• The height of the tree (height of the root node) is 2.
• The height of the node 5 is one.

What is the maximum and minimum height of the binary tree having n elements?

The height of the binary tree can always be in the range of log(n) to (n-1).

• If the BT is fully balanced (every node has zero or two nodes), the height of the tree is log(n).
• If every node in the binary tree has only one node attached, the height of the BT is (n-1).

For example, the binary tree having eight nodes can have minimum height log(8)=3 and maximum height 8-1=7 nodes.

You can find the height of the binary tree using recursion technique.

Using recursion, it is simple. The height of any node (root) is one plus maximum of the height of the left and right node.

Python Program to find the Height of the Binary Tree:

class node:
    def __init__(self, val, left=None, right=None):
        self.left=left
        self.val=val
        self.right=right

def height(root):
    if root:
        return 1+max(height(root.left), height(root.right))
    else:
        return -1

root=node(4)
root.left=node(1)
root.right=node(5)
root.left.left=node(7)
root.left.right=node(3)
root.right.right=node(6)

print("Height of the Binary Tree: ", height(root))

Output:

Height of the Binary Tree:  2

If there is no right or left child to the root node, the height of the BT will be zero.

You can write a program to find the height of the Binary Tree in any programming languages like C/C++, Java using the same logic.

Knowing the height of the binary tree is very important to solve many of the binary tree problems in competitive programming.