[Solved] Print All Ancestors of a Given Node in the Binary Tree

What are Ancestors in Binary Tree?

The ancestors of any given node are nothing but the parent, grandparent, and great-grandparent and so on…

Example:

Let’s take the following Binary Tree example.

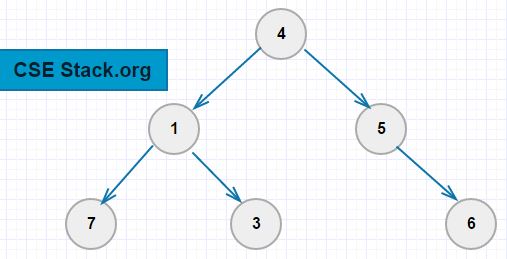
The ancestors of node 3 are 1, 4.
The ancestors of node 6 are 5, 4.

Nodes 7 and 3 have the same ancestors- parent (1) and grandparent (4).

The node ‘x’ is the parent of ‘y’ if ‘y’ is present either on the left side or the right side of ‘x’.

All the ancestors of the parent node are also the ancestors of the child node.

Let’s see the code to print and find all ancestors of a given node in the binary tree.

(This problem is an extension of the program to find the parent of the node in a binary tree. Try this first.)

Python Program

Here is the recursive solution to find all the ancestors of the given node in the tree.

You can implement the same logic to solve this problem in any other programming language like C/C++, Java…

Python code:

	
#binary tree node structure
class node:
  def __init__(self, val, left=None, right=None):
    self.left=left
    self.val=val
    self.right=right


#function to print all the ancestors of a given node
def findAncestors(root, val):
  if not root:
    return False
  else:
    if root.val==val:
      return True
    else:
      if findAncestors(root.left,val) or findAncestors(root.right,val):
        print(root.val)
        return True

#create binary tree
root=node(4)
root.left=node(1)
root.right=node(5)
root.left.left=node(7)
root.left.right=node(3)
root.right.right=node(6)
 
print("Ancestors of 6:")
findAncestors(root, 6)

Output:

Ancestors of 6:
5
4

Complexity

Each node in the binary tree is visited at once. The complexity of the above program is O(n) where ‘n’ is the number of nodes in the binary tree.

This is all about finding and printing the ancestors of a given node in the binary tree.

If you are preparing for competitive programming, there can be multiple questions you will be asked like finding the lowest common ancestors for given two nodes. (This question was asked to me in Amazon interview.)