In this article, you will learn detail about heap data structure. Detail includes- the difference between min heap and max heap, their usage, and different insertion and deletion operations.
Table of Contents:
Heap is a specialized data structured, basically based on the tree data structure that satisfies the heap property.
Heap Property:
Suppose node A is a parent of node B, there is a special ordering of the value of node A with respect to the value of node B.
This heap property applies across the heap for every parent-child node pairs.
Heap has a special property. That makes it differ from Tree. Suppose there is any parent node A and child node B, there need to be in the specific ordering of the values of A and B. The ordering of value can be increasing or decreasing order. According to the ordering of parent and child node value, there are two types of heap data structure:
This ordering is not necessary for a tree data structure.
The ordering of the values can be increasing or decreasing order. According to the ordering of parent and child node values, there are two types of heap data structure:
Let’s see Min and Max heap one-by-one. In the end, you will understand the major difference between the two.
In min heap, for every pair of the parent and descendant child node, the parent node has always lower value than descended child node.
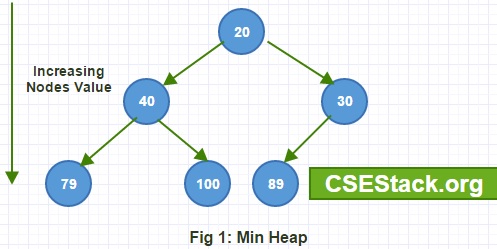
The value of the nodes increases as we traverse from root to leaf node.
The root node has the lowest value.
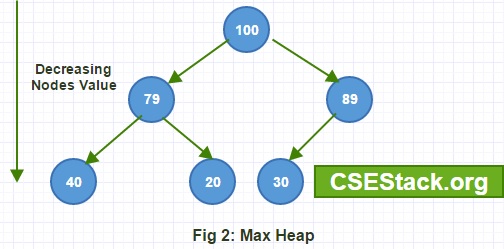
In the max heap, for every pair of the parent and descendant child node, the parent node has always greater value than descended child node.
The value of the nodes decreases as we traverse from root to leaf node.
The root node has the greatest value.
There are multiple operations that carried out on heap data structure such as heap creation, selection, insertion, and deletion of a node from the heap.
While inserting or deleting a node from the heap, there is a need to maintain the heap property, this is carried out by the basic operation called Heapify.
Add a given element that needs to Heapify, at the root node. If root node value is greater than its left and right child, terminate. Else replace root node value with the greatest value of left and right child. Continue Heapify for same element node at the next level by considering it as the root node.
Note: Above Heapify algorithm is to Heapify element for the max heap. For min heap, root node value has to replace with the lowest value of the left and right child.
Add element at the end of Heap (Tree) Apply reverse Heapify method from bottom to root node.
Insertion operation involves heapify operation and it takes time depending upon the height of the tree. For n elements, the height of the binary complete tree is (nLogn). So complexity to insert the element in the heap is O(nLogn).
In the case of max heap, maximum number value node will be the root node. So we can find it in constant time i.e. O(1).
This is the same case for finding the minimum value in min heap.
Select the root node as it max value in a max heap. Replace the root node with the last node of the heap. Heapify the newly selected root node.
Selecting the root node and replacing it with the last node, takes constant time. So the complexity of deleting a maximum element from the heap is same as heapify operation i.e. O(nLogn).
Find the following table for Heap operation complexity for insert, find and delete operations.
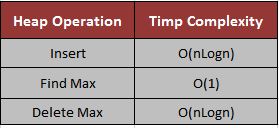
Note: This complexity is according to the operation on the Max Heap Data Structure.
O(1) to find the greatest number from the array. (Max heap have the greatest value at root node)O(1) to find the lowest number from the array. (Min heap have the lowest value at the root node).O(nLogn) for sorting.Is Heap sorted?
Heap is partially sorted as it maintains ordering between parent and child node. It is not completely sorted as there is no specific ordering between sibling nodes.
What is the difference between min heap and max heap?
Hope you find the answer in this article for this question.
How to implements min and max heap in programming like C/Java?
Just like tree implementation, you can implement heap using Linked List data structure.
Each node in the Linked List will be having two links pointing to the two children nodes.
Is heap complete binary tree?
Yes, it is the complete binary tree.
What is the order of the sibling elements (elements at the same level) in heap?
There is no ordering between nodes at the same level (Sibling nodes).
Is heap similar to the stack or queue?
No way.
Many gets confuse and correlate heap with stack or queue.
Remember stack and queue are abstract data type while heap is the actual data structure.
If you have any further point to discuss on min heap and max heap, feel free to ask your doubt by commenting below.
I am a Python enthusiast who loves Linux and Vim. I hold a Master of Computer Science degree from NIT Trichy and have 10 years of experience in the IT industry, focusing on the Software Development Lifecycle from Requirements Gathering, Design, Development to Deployment. I have worked at IBM, Ericsson, and NetApp, and I share my knowledge on CSEstack.org.
Insertion and deletion of an element takes log(n) and not nlog(n) as mentioned above. The problem space gets divided in half in every iteration of heapify.