The tree is an important data structure. It has a parent and children relationship at various levels.
In this article, we are more focusing on tree traversing. You will also learn different types of binary tree traversal algorithm.
Table of Contents
It is a special type of tree.
The binary tree is tree data structure which has at most two children for every node.
Here left and right children nodes are distinct.

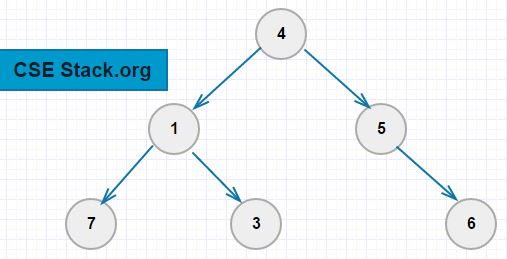
In the above tree diagram, the node with value ‘4’ is the root node. It has two children nodes with the values ‘1’ and ‘3’.
This is another diagram and example where a binary tree is used to find the Fibonacci number series.
Don’t think about it right now. we will see the Fibonacci number series later as it is out of the scope of this article.
In the tree, the address of the root node is only accessible to us. We can not access any other nodes directly.
If you want to visit any node, the only way is to travel the tree.
First, visit the root node, find their children nodes, then grandchildren nodes and so on…
To visit all the notes, there is a certain pattern is followed to visit all the nodes on the given tree. The type of flow or pattern used to visit the node in the tree is called the tree traversing algorithm.
Unlike other data structures such as an array, stack, queue, linked list; there are are many ways to traverse the elements of the binary tree. In this post, we see various types of binary tree traversal with its algorithm.
There are 3 standard types of depth search binary tree traversal and one breath search binary tree traversal.
In this article, we are looking at the depth search level algorithm.
Let’s look at the different Depth Search Level order binary tree traversal one-by-one.
Note: While going through different binary tree traversal algorithm, we will refer the following diagram as an example.

Traversing algorithms can be implemented using recursion technique or loop.
The first node will be visited then it will traverse to left subtree and then right subtree.
Algorithm Preorder(tree) Visit root node of the tree call preorder(left subtree) //recursion call call preorder(right subtree) //recursion call
Example: The preorder traversal of the above tree is 4 1 7 3 5 6.
Use of Preorder Traversal:
Preorder traversal can be used to find out the polish notation of the expression. Polish notation is useful to evaluate the expression effectively.
The left subtree will be traversed first, then the root node will be visited. After that, it will call to right subtree.
Algorithm Inorder(tree) call inorder(left subtree) //recursion call Visit the root node of the tree call inorder(right subtree) // recursion call
Example: If we find the inorder traversal of the above tree, it will be 7 1 3 4 5 6.
Use of inorder traversal:
If we apply the inorder traversal on binary search tree it will give numbers in ascending order. So the inorder traversal is used to find the numbers in increasing order for binary search tree.
The left subtree and then the right subtree will be traversed first. After that, the root node will be visited.
Algorithm Postorder(tree) call postorder(left subtree) // recursion call call postorder(right subtree) // recursion call Visit the root node of the tree
Example: The postorder traversal of the above tree is 7 3 1 6 5 4.
Use of postorder traversal:
It is used to find out postfix expression. It is also useful for deleting nodes in the linked list. As elements at the bottom get deleted first, the structure of the tree after deletion of the bottom node will get preserved.
class node:
def __init__(self, val, left=None, right=None):
self.left=left
self.val=val
self.right=right
def traverseInOrder(root):
if root:
traverseInOrder(root.left)
print(root.val)
traverseInOrder(root.right)
def traversePreOrder(root):
if root:
print(root.val)
traversePreOrder(root.left)
traversePreOrder(root.right)
def traversePostOrder(root):
if root:
traversePostOrder(root.left)
traversePostOrder(root.right)
print(root.val)
root=node(4)
root.left=node(1)
root.right=node(5)
root.left.left=node(7)
root.left.right=node(3)
root.right.right=node(6)
print("Preorder Traversal of Binary Tree:")
traversePreOrder(root)
print("Preorder Traversal of Binary Tree:")
traverseInOrder(root)
print("Preorder Traversal of Binary Tree:")
traversePostOrder(root)
Output:
Preorder Traversal of Binary Tree: 4 1 7 3 5 6 Preorder Traversal of Binary Tree: 7 1 3 4 5 6 Preorder Traversal of Binary Tree: 7 3 1 6 5 4
Wrapping up…
The binary tree traversal algorithm is also used in the min-max heap data structure.
I see a lot of questions related to the tree traversing asked in many of the interviews. So, understand it very well.
If you have any questions related to Preorder, inorder and postorder depth-first search traversal, write a comment below.
I was just looking for Binary Tree Traversal and happy to find it on Google. Its nice content.
Thanks Natalie! I am glad as you find it useful.
hello hello!nice
Thanks 🙂
Helpful!
I’m glad. Thanks!