Problem statement: Write a program to find the longest/maximum path in a weighted tree.
This coding question was asked in one of the coding interview rounds.
It is a tree in which every edge will be assigned with a number. It is also called edge distance between two connected nodes.
Example:
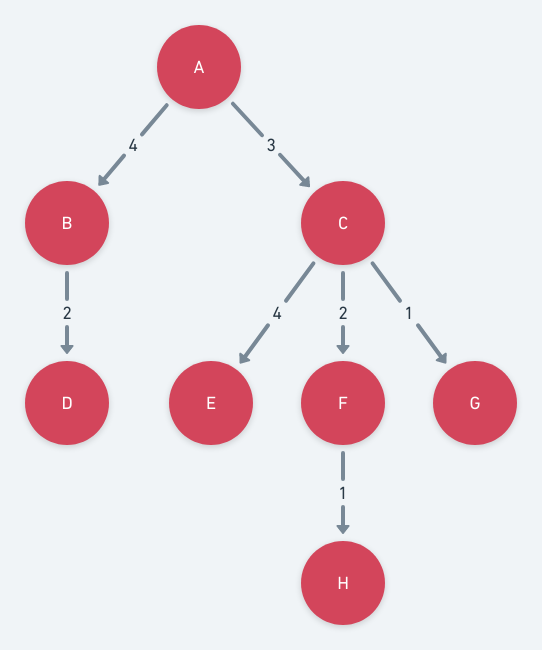
In the above tree example: The weight of the edge connecting nodes ‘A’ and ‘B’ is 4. Similarly, The weight of the edge connecting nodes ‘C’ and ‘F’ is 4.
The longest path in a weighted tree is 7 (4+3) from node ‘A’ to ‘C’ (A-C-E).
Here is a simple program to create a weighted tree and find the longest path.
#tree node
class node:
def __init__(self, intVal, listPtr=None):
self.intVal=intVal
self.listPtr=listPtr
#find max path in weighted tree
def maxPath(root):
if root:
if not root.listPtr:
return root.intVal
else:
return root.intVal+max([maxPath(i) for i in root.listPtr])
#create weighted tree
root=node(0,[node(4,[node(2)]),node(3,[node(4),node(2,[node(1)]),node(1)])])
#print maximum path of weighted tree
print(maxPath(root))
The class node is used to save the data for each tree node.
The class variable intVal is used to save the edge value from its parent. For example, the value of intVal for node ‘C’ is 3, for node ‘E’ is 4 and for node ‘A’ (root node) is 0 (zero).
A listPtr is the Python list object. It will save the addresses of all the child nodes.
To find the max path in the weighted tree, we are using the recursion mechanism.
You can solve these coding challenges in any programming language like C/C++, Java or Python. In other programming languages, there will be syntax differences. Logic will be the same.
In this tutorial, you learn to code for a weighted tree and find a maximum path in a weighted tree. If you have any questions or if you find any better solution, write in the comment.
Check competitive coding questions on the binary tree for practice if you are preparing for top product-based companies.
I am complete Python Nut, love Linux and vim as an editor. I hold a Master of Computer Science from NIT Trichy. I dabble in C/C++, Java too. I keep sharing my coding knowledge and my own experience on <b>CSEstack.org</b> portal.
Do you want me to send you programing updates for FREE?
Subscribe below…
#tree node class node: def __init__(self, intVal, listPtr=None): self.intVal=intVal self.listPtr=listPtr #find max path in weighted tree def maxPath(root): #checks if root is present if root: if not root.listPtr: return root.intVal else: return root.intVal+max([maxPath(i) for i in root.listPtr]) d=node(2) b=node(4,[d]) #children of f h=node(1) #children of c e=node(4) f=node(2,[h]) g=node(1) c=node(3,[e,f,g]) # a is root a=node(0,[b,c]) #print maximum path of weighted tree print(maxPath(a))